Hello, I am working with 10x Genomics scRNA-seq data. I am using Seurat::CellCycleScoring() to assign cell cycle stages to cells and
later batchelor::regressBatches() to remove this unwanted source of variation.
My question is regarding output from regressBatches().
As documentation says, the output is "A SingleCellExperiment object containing the corrected assay.",
where corrected assay is object of class ResidualMatrix,
and "the residuals represent the expression values after correcting for the batch effect".
I am really not sure if I am using the ResidualMatrix properly in downstream analyses.
I have used this matrix to calculate dimreds, clustering and to find cluster markers.
Although I can see that some genes are relatively good markers (log2FC > 1, FDR < 0.1; Seurat::FindAllMarkers() using Wilcox test),
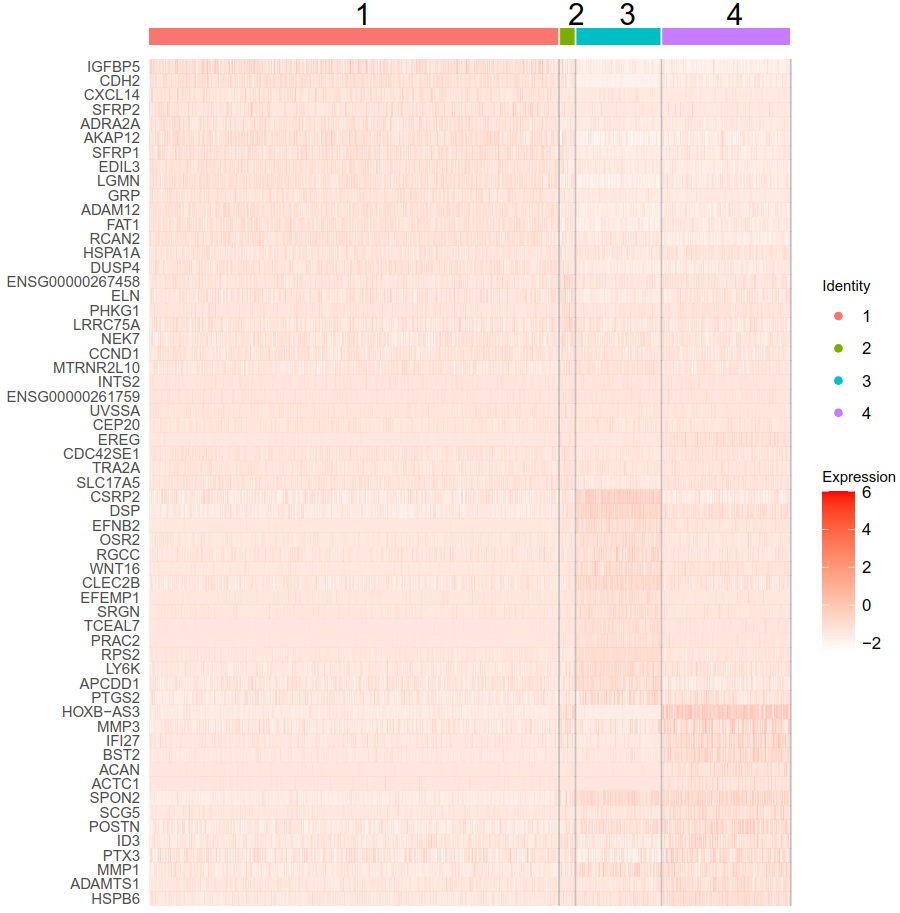
the heatmap of such genes is not very convincing (see below - top 15 upregulated genes from each cluster).
For example, the first gene (IGFBP5) has log2FC of 2.2 in the first cluster, but I can barely see a difference in the heatmap.
I am not sure if this is just caused by improper color gradient, but you can see that are negative values in the ResidualMatrix.
TLDR: Can I use ResidualMatrix obtained from
regressBatches()
in the same way as e.g. corrected UMI matrix obtained from Seurat::SCTransform() (both used to remove cell cycle effect)?
Thanks in advance for reply!


Many thanks Aaron! Especially your comment about "the dangers of regression in single-cell applications" was quite useful for me, as I was not fully aware of potential troubles. After further reading of this chapter in OSCA and this and this question, I am more convinced that in my case, regression was not the ideal tool for dealing with cell cycle effects.
I will try to use the "CC driver genes removal strategy" described here (or alternatively in a comment of the second question above).