You are asking about an interaction term, which is (drug-continued - control1) - (drug-withdrawed - control2), which assumes that there are actual differences between the two control samples. If the two controls are essentially the same thing, they cancel out and then it's just drug-continued - drug-withdrawed.
There's probably a more automatic way of doing this, but I don't totally get how DESeq2 does the contrasts, so I do it the dumb direct way. As a fake example
> dds <- makeExampleDESeqDataSet()
> design(dds)
~condition
> colData(dds)
DataFrame with 12 rows and 1 column
condition
<factor>
sample1 A
sample2 A
sample3 A
sample4 A
sample5 A
... ...
sample8 B
sample9 B
sample10 B
sample11 B
sample12 B
## change this to have four levels
> colData(dds) <- DataFrame(condition = factor(rep(LETTERS[1:4], each = 3)))
> colData(dds)
DataFrame with 12 rows and 1 column
condition
<factor>
1 A
2 A
3 A
4 B
5 B
... ...
8 C
9 C
10 D
11 D
12 D
## and change to a cell means model, which isn't totally necessary, but maybe easier to understand
> design(dds) <- ~ 0 + condition
> design(dds)
~0 + condition
> dds <- DESeq(dds)
estimating size factors
estimating dispersions
gene-wise dispersion estimates
mean-dispersion relationship
final dispersion estimates
fitting model and testing
## the signs in the interaction term I described above, after
## distributing into the parentheses are 1, -1, -1, 1
## so we use that as the contrast
> results(dds, c(1, -1, -1, 1))
log2 fold change (MLE): +1,-1,-1,+1
Wald test p-value: +1,-1,-1,+1
DataFrame with 1000 rows and 6 columns
baseMean log2FoldChange
<numeric> <numeric>
gene1 88.17007 0.895912
gene2 11.37401 0.267528
gene3 10.31525 -3.993132
gene4 2.00921 0.069651
gene5 18.40443 -0.322246
... ... ...
gene996 13.0700 1.448528
gene997 14.3798 0.200951
gene998 79.2857 -0.550139
gene999 16.5750 -0.014954
gene1000 14.8213 -2.309181
lfcSE stat
<numeric> <numeric>
gene1 0.592058 1.5132152
gene2 1.463057 0.1828555
gene3 1.442082 -2.7690057
gene4 2.609663 0.0266897
gene5 1.069997 -0.3011655
... ... ...
gene996 0.992003 1.4602058
gene997 1.149728 0.1747813
gene998 0.633383 -0.8685729
gene999 1.124772 -0.0132952
gene1000 1.049954 -2.1993176
pvalue padj
<numeric> <numeric>
gene1 0.13022500 0.852226
gene2 0.85491143 0.998859
gene3 0.00562277 0.763831
gene4 0.97870726 0.998859
gene5 0.76328833 0.998859
... ... ...
gene996 0.1442335 0.852768
gene997 0.8612515 0.998859
gene998 0.3850808 0.979411
gene999 0.9893923 0.998859
gene1000 0.0278553 0.763831


Thanks for the answer,
I'll check the links thanks again.
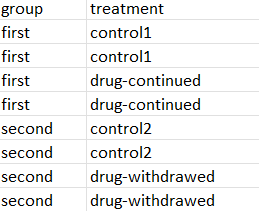
As there is a technical difference between group 1 and 2 (run time) so it is a batch.
In that case I believe this is what you are looking for: 2 controls and 2 conditions
It will be something like the following:
Assuming you have a summarized experiment object:
It may not be exactly right, but you are not too far off now. IF it were me I would be using the contraster() function of the blog post above to make sure I was comparing exactly as I thought.
Thank you, this was what I want.
I want to ask one additional question, if the two controls are the same in that case the equation becomes (dc-c1) - (dw-c1). In that scenario, since two controls are the same do they cancel out each other? If so, how can I use one control as baseline but compare my two groups (dc and dw)?
First, the 2 controls are different because they were run at different time points. However, if they were hypothetically identical, then there would be only 1 control (as you call it "c1"). Then it would be (dc-c1) - (dw-c1) as you suggest. So in an equation: yes they cancel each other. But that does not mean nothing happened, it means the same thing was subtracted from both.
EDIT: This following paragraph is not right, thanks James: - Mathematically, this is what is happening: Consider 2 fruit bags, both contain apples (treatment) and oranges (control). I don't care about the total number in each bag, only the number of apples. So bag1-bag2 (or dc-dw) is not what I want, unless I first remove the oranges (dc-c1)-(dw-c1). Ridiculous example I know, but it's friday!
I find it easier to conceptualise interactions not as equations but as "difference between differences":
How can I use one control as baseline but compare my two groups (dc and dw)?
Thanks a lot !!!
Mathematically it doesn't matter if you remove the oranges or not. Say there are 8 apples in one bag and 3 in the other. The difference will be 5 no matter how many oranges are in the bags, because it's the same number of oranges! That's what it means to say they cancel each other out. In other words, dc - dw is exactly what you want because it's identical to (dc - c1) - (dw - c1), for any value of c1.
Yup.
So that means there is no need for an interaction term in the design for this scenario of 2 conditions + 1 control.
Thanks James, so easy to go wrong with this.
If there are 4 +- 2.0 oranges in the control bag and 8 +- 0.5 in bag 1 and 3 +- 0.2 in bag2, and you are trying to compare bag 1 to the control bag, and then bag 2 to the control bag, and then want to compare the comparisons, you've got a huge headache on your hands would not have had if you had just compared bag 1 to bag 2.
Adding in the inherent uncertainty of the controls makes things worse.