Question

Overfitting in limma

0

Entering edit mode

Marek Gierlinski ▴ 30

@mgierlinski-7369

Last seen 5 months ago

United Kingdom

I have a data from a large proteomics study from 237 patients. It is a time course (days 1, 4, 8, 15 and 29) in two treatments: drug and placebo. The data were collected in several batches. We know age and sex of each patient.

Initially I run limma using a model

~ treatment + day + batch + age_group + sex

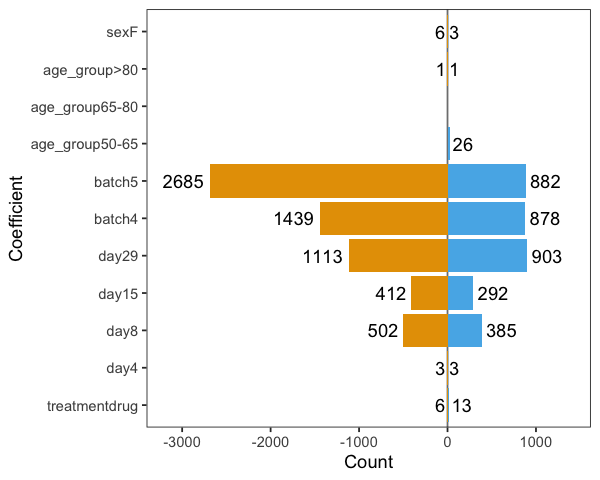
It shows very strong batch effects. The figure below shows the numbers of statistically significant proteins (going up - blue, and down - orange) at FDR < 0.01 level:

Significant proteins for a simpler model

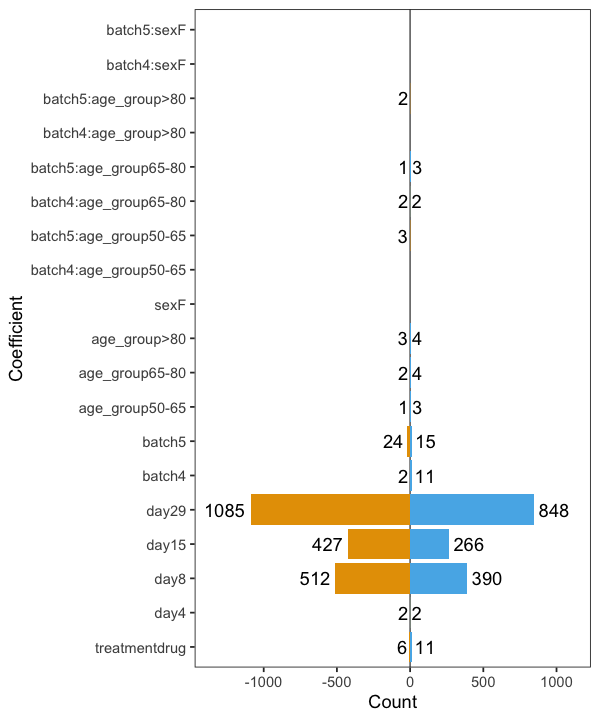
However, I found that age and sex distribution is significantly different between the batches, so I want to include interaction terms. When I use a model

"~ treatment + day + batch * (age_group + sex)

batch effects suddenly almost disappear.

Significant proteins for complex model

This is very nice and, if batch effects are caused by age and sex distribution, that would explain my data. On the other hand, the interaction terms contain only a few significant proteins.

I am worried that at this point I am overfitting the data with too many coefficients and the model is too good to be true. Is there a way of finding if the model overfits data in limma?

Note: the input for limma is a matrix with 237 columns (samples) and 5839 rows (proteins). As data are confidential, I cannot present all of it here.

limma Regression overfitting • 1.5k views

ADD COMMENT • link updated 2.5 years ago by Gordon Smyth 51k • written 2.6 years ago by Marek Gierlinski ▴ 30

score 1 · Answer 1 · 2022-05-05

1

Entering edit mode

Gordon Smyth 51k

@gordon-smyth

Last seen 1 hour ago

WEHI, Melbourne, Australia

The batch effects haven't disappeared, you just can't see them in a list of DE genes for the individual batch effect terms. If you did a limma test for all the batch effects together, then you would find that the significant batch effects are still there.

You have almost certainly over-parameterized the batch effects by introducing more coefficients than is needed to capture them. The first model therefore would probably be better. But it doesn't really matter. limma will do the adjustment either way, taking into account any overlap of coefficients. As you can see, the DE lists for your factors of interest, treatment and time, remain very similar regardless of which model you use. limma will do the test for the factors of interest correctly, regardless of whether your model has a few extra coefficients or not.

ADD COMMENT • link 2.6 years ago Gordon Smyth 51k

0

Entering edit mode

Thank you, Gordon. Is there any formal way of comparing "full" and "reduced" models in limma? In linear regression one can find SSE and d.o.f. for each model and perform an F-test. If I understand correctly, lmFit fits a linear model to each gene. Is it possible to get a summary statistic for all models analogous to F in one regression?

ADD REPLY • link 2.6 years ago Marek Gierlinski ▴ 30

1

Entering edit mode

In limma, you do an F-test simply by specifying multiple coeffcients to topTable. limma then does an F-test for all the specified coefficients. The "full" model if the one with all the coefficient in. The "reduced" model is the one with all the specified coeffcients removed, or set to zero. If you want an F-test for the overall model, then specify all the coefficents (excluding the intercept).

ADD REPLY • link 2.5 years ago Gordon Smyth 51k

0

Entering edit mode

By the way, I looked at the distribution of p-values in both models, and while the simpler model gives nice uniform distributions with some excess in small values, in the complex model age, sex and interaction terms have a reversed p-value distribution - increasing towards larger values. This seems to confirm that the complex model is not appropriate here.

ADD REPLY • link 2.6 years ago Marek Gierlinski ▴ 30